3 Roulette
Roulette Table
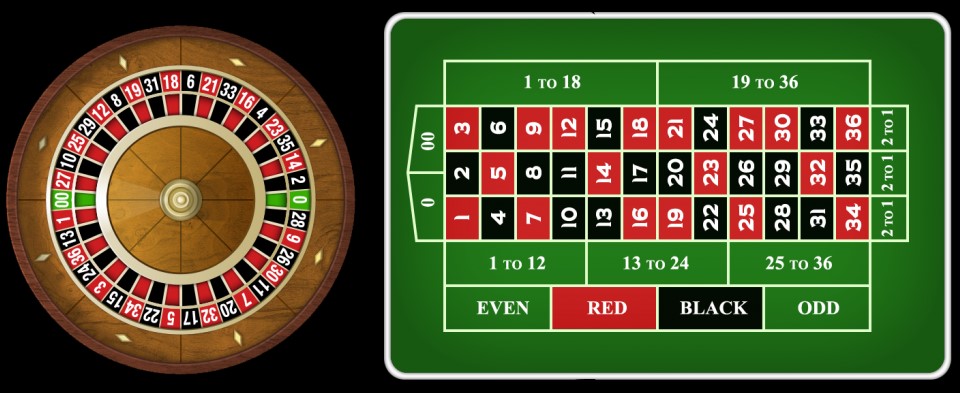
Roulette is a fun and simple game where a large wheel is spun and then a ball is dropped into the wheel. Players bet on where the ball will land. The main numbers range from 1 to 36 and are divided into half red and half black. There is also an additional number: zero that is neither red nor black (nor is it even or odd). In most games, you will find zero (0) and double zero (00). The presence of these numbers is what gives the house its edge in the game.
There are a variety of bets that can be made in Roulette:
- Red or black, paying 1-to-1
- Even or odd, paying 1-to-1
- Any single number (“Straight Up”), paying 35-to-1
- Two adjacent numbers (“Split”), paying 17 to 1
- Three numbers in a row (“Street”), paying 11 to 1
- Four adjoining numbers (“Corner”), paying 8 to 1
- Twelve numbers, either sequential (“Dozen”) or in a “Column”, paying 2 to 1
- 1-18 or 19-36, paying 1-to-1
Interestingly, the expected return on all of these bets is exactly the same. To show why this is true, let’s calculate a few. First, we’ll calculate my favorite bet: red or black, paying even money.
\[ Expected Value = \frac{18}{38} * (\$1) + \frac{20}{38} * (-\$1) = -\frac{2}{38} = -0.05263158 \]
Notice that this bet is almost like flipping a coin (1). In fact, if the zeroes were not on the board and we only had 36 numbers, it would be identical. However, the presence of the zeroes means that we have 38 outcomes, not 36, and the 2 new outcomes that are introduced by the presence of the zero are losses for us. This turns the expected return slightly negative, giving the house a 5.26% edge. However much money we place on this bet, we should expect to lose an average of 5.26% with each spin of the wheel.
Let’s calculate another one. Obviously, the even or odd bet will be the same. So let’s do a straight up bet on a single number. The expected return in this case is:
\[ Expected Value = \frac{1}{38} * (\$35) + \frac{37}{38} * (-\$1) = -\frac{2}{38} = -0.05263158 \]
As suggested, this is the the same house edge as the red/black or even/odd bet. Knowing that the payout on any bet is equal to the true odds in the absence of the zeroes, we can see that this will always come out the same way. Just to demonstrate this, here are the expected values for bets place on 4 and 12 numbers:
\[ Expected Value = \frac{4}{38} * (\$8) + \frac{34}{38} * (-\$1) = -\frac{2}{38} = -0.05263158 \]
\[ Expected Value = \frac{12}{38} * (\$2) + \frac{26}{38} * (-\$1) = -\frac{2}{38} = -0.05263158 \]
So far we have analyzed “American” roulette, which has both zero and double zero. “European” roulette instead only has 1 zero. Intuitively, we know that this will improve our odds. Specifically, we find that a single number bet now has the expected value:
\[ Expected Value = \frac{1}{37} * (\$1) + \frac{36}{37} * (-\$1) = -\frac{1}{37} = -0.02702703 \]
The house edge has been cut almost in half, from 5.26% to 2.70%. As with “American” roulette, all of the other bets will have this same expected value and house edge. Obviously, it is advantageous to players to play at “European” style tables whenever possible.